NCERT Solutions Class 9 Maths Chapter 12 – Download Free PDF
*According to the CBSE Syllabus 2023-24, this chapter has been renumbered as Chapter 10.
NCERT Solutions for Class 9 Maths Chapter 12 – Heron’s Formula is provided here. Heron’s formula is a fundamental concept that finds significance in countless areas and is included in the CBSE Syllabus of Class 9 Maths. Therefore, it is imperative to have a clear grasp of the concept. And one of the best ways to do just that is by referring to the NCERT Solutions for Class 9 Maths Chapter 12 Heron’s Formula. These solutions are designed by knowledgeable teachers with years of experience in accordance with the latest update on the CBSE syllabus 2023-24. The NCERT Solutions for Class 9 aim at equipping the students with detailed and step-wise explanations for all the answers to the questions given in the exercises of this Chapter.
Hence, one of the best guides you could adapt to your study needs is NCERT Solutions. Relevant topics are presented in an easy-to-understand format, barring the use of any complicated jargon. Furthermore, its content is updated as per the last CBSE syllabus and its guidelines.
Download PDF of NCERT Solutions Class 9 Maths Chapter 12 Heron’s Formula
List of Exercises in NCERTclass 9 Maths Chapter 12:
Access Answers of NCERT Class 9 Maths Chapter 12 – Heron’s Formula
Exercise: 12.1 (Page No: 202)
1. A traffic signal board, indicating ‘SCHOOL AHEAD’, is an equilateral triangle with side ‘a’. Find the area of the signal board, using Heron’s formula. If its perimeter is 180 cm, what will be the area of the signal board?
Solution:
Given,
Side of the signal board = a
Perimeter of the signal board = 3a = 180 cm
∴ a = 60 cm
Semi perimeter of the signal board (s) = 3a/2
By using Heron’s formula,
Area of the triangular signal board will be =


2. The triangular side walls of a flyover have been used for advertisements. The sides of the walls are 122 m, 22 m and 120 m (see Fig. 12.9). The advertisements yield an earning of ₹5000 per m2 per year. A company hired one of its walls for 3 months. How much rent did it pay?

Solution:
The sides of the triangle ABC are 122 m, 22 m and 120 m respectively.
Now, the perimeter will be (122+22+120) = 264 m
Also, the semi perimeter (s) = 264/2 = 132 m
Using Heron’s formula,
Area of the triangle =

=1320 m2
We know that the rent of advertising per year = ₹ 5000 per m2
∴ The rent of one wall for 3 months = Rs. (1320×5000×3)/12 = Rs. 1650000

3. There is a slide in a park. One of its side walls has been painted in some colour with a message “KEEP THE PARK GREEN AND CLEAN” (see Fig. 12.10 ). If the sides of the wall are 15 m, 11 m and 6 m, find the area painted in colour.

Solution:
It is given that the sides of the wall as 15 m, 11 m and 6 m.
So, the semi perimeter of triangular wall (s) = (15+11+6)/2 m = 16 m
Using Heron’s formula,
Area of the message =

= √[16(16-15)(16-11) (16-6)] m2
= √[16×1×5×10] m2 = √800 m2
= 20√2 m2

4. Find the area of a triangle two sides of which are 18 cm and 10 cm and the perimeter is 42cm.
Solution:
Assume the third side of the triangle to be “x”.
Now, the three sides of the triangle are 18 cm, 10 cm, and “x” cm
It is given that the perimeter of the triangle = 42cm
So, x = 42-(18+10) cm = 14 cm
∴ The semi perimeter of triangle = 42/2 = 21 cm
Using Heron’s formula,
Area of the triangle,
=

= √[21(21-18)(21-10)(21-14)] cm2
= √[21×3×11×7] m2
= 21√11 cm2

5. Sides of a triangle are in the ratio of 12 : 17 : 25 and its perimeter is 540cm. Find its area.
Solution:
The ratio of the sides of the triangle are given as 12 : 17 : 25
Now, let the common ratio between the sides of the triangle be “x”
∴ The sides are 12x, 17x and 25x
It is also given that the perimeter of the triangle = 540 cm
12x+17x+25x = 540 cm
54x = 540cm
So, x = 10
Now, the sides of triangle are 120 cm, 170 cm, 250 cm.
So, the semi perimeter of the triangle (s) = 540/2 = 270 cm
Using Heron’s formula,
Area of the triangle

= 9000 cm2

6. An isosceles triangle has perimeter 30 cm and each of the equal sides is 12 cm. Find the area of the triangle.
Solution:
First, let the third side be x.
It is given that the length of the equal sides is 12 cm and its perimeter is 30 cm.
So, 30 = 12+12+x
∴ The length of the third side = 6 cm
Thus, the semi perimeter of the isosceles triangle (s) = 30/2 cm = 15 cm
Using Heron’s formula,
Area of the triangle
=

= √[15(15-12)(15-12)(15-6)] cm2
= √[15×3×3×9] cm2
= 9√15 cm2
Exercise: 12.2 (Page No: 206)
1. A park, in the shape of a quadrilateral ABCD, has C = 90°, AB = 9 m, BC = 12 m, CD = 5 m and AD = 8 m. How much area does it occupy?
Solution:
First, construct a quadrilateral ABCD and join BD.
We know that
C = 90°, AB = 9 m, BC = 12 m, CD = 5 m and AD = 8 m
The diagram is:

Now, apply Pythagoras theorem in ΔBCD
BD2 = BC2 +CD2
⇒ BD2 = 122+52
⇒ BD2 = 169
⇒ BD = 13 m
Now, the area of ΔBCD = (½ ×12×5) = 30 m2
The semi perimeter of ΔABD
(s) = (perimeter/2)
= (8+9+13)/2 m
= 30/2 m = 15 m
Using Heron’s formula,
Area of ΔABD

= 6√35 m2 = 35.5 m2 (approximately)
∴ The area of quadrilateral ABCD = Area of ΔBCD+Area of ΔABD
= 30 m2+35.5m2 = 65.5 m2

2. Find the area of a quadrilateral ABCD in which AB = 3 cm, BC = 4 cm, CD = 4 cm, DA = 5 cm and AC = 5 cm.
Solution:
First, construct a diagram with the given parameter.

Now, apply Pythagorean theorem in ΔABC,
AC2 = AB2+BC2
⇒ 52 = 32+42
⇒ 25 = 25
Thus, it can be concluded that ΔABC is a right angled at B.
So, area of ΔBCD = (½ ×3×4) = 6 cm2
The semi perimeter of ΔACD (s) = (perimeter/2) = (5+5+4)/2 cm = 14/2 cm = 7 m
Now, using Heron’s formula,
Area of ΔACD

= 2√21 cm2 = 9.17 cm2 (approximately)
Area of quadrilateral ABCD = Area of ΔABC + Area of ΔACD = 6 cm2 +9.17 cm2 = 15.17 cm2
3. Radha made a picture of an aeroplane with coloured paper as shown in Fig 12.15. Find the total area of the paper used.

Solution:
For the triangle I section:

It is an isosceles triangle and the sides are 5 cm, 1 cm and 5 cm
Perimeter = 5+5+1 = 11 cm
So, semi perimeter = 11/2 cm = 5.5 cm
Using Heron’s formula,
Area = √[s(s-a)(s-b)(s-c)]
= √[5.5(5.5- 5)(5.5-5)(5.5-1)] cm2
= √[5.5×0.5×0.5×4.5] cm2
= 0.75√11 cm2
= 0.75 × 3.317cm2
= 2.488cm2 (approx)
For the quadrilateral II section:
This quadrilateral is a rectangle with length and breadth as 6.5 cm and 1 cm respectively.
∴ Area = 6.5×1 cm2=6.5 cm2
For the quadrilateral III section:
It is a trapezoid with 2 sides as 1 cm each and the third side as 2 cm.
Area of the trapezoid = Area of the parallelogram + Area of the equilateral triangle
The perpendicular height of the parallelogram will be

= 0.86 cm
And, the area of the equilateral triangle will be (√3/4×a2) = 0.43
∴ Area of the trapezoid = 0.86+0.43 = 1.3 cm2 (approximately).
For triangle IV and V:
These triangles are 2 congruent right angled triangles having the base as 6 cm and height 1.5 cm
Area triangles IV and V = 2×(½×6×1.5) cm2 = 9 cm2
So, the total area of the paper used = (2.488+6.5+1.3+9) cm2 = 19.3 cm2
4. A triangle and a parallelogram have the same base and the same area. If the sides of the triangle are 26 cm, 28 cm and 30 cm, and the parallelogram stands on the base 28 cm, find the height of the parallelogram.
Solution:
Given,
It is given that the parallelogram and triangle have equal areas.
The sides of the triangle are given as 26 cm, 28 cm and 30 cm.
So, the perimeter = 26+28+30 = 84 cm
And its semi perimeter = 84/2 cm = 42 cm
Now, by using Heron’s formula, area of the triangle =

= √[42(42-26)(42-28)(42-30)] cm2
= √[42×16×14×12] cm2
= 336 cm2
Now, let the height of parallelogram be h.
As the area of parallelogram = area of the triangle,
28 cm× h = 336 cm2
∴ h = 336/28 cm
So, the height of the parallelogram is 12 cm.

5. A rhombus shaped field has green grass for 18 cows to graze. If each side of the rhombus is 30 m and its longer diagonal is 48 m, how much area of grass field will each cow be getting?
Solution:
Draw a rhombus-shaped field first with the vertices as ABCD. The diagonal AC divides the rhombus into two congruent triangles which are having equal areas. The diagram is as follows.

Consider the triangle BCD,
Its semi-perimeter = (48 + 30 + 30)/2 m = 54 m
Using Heron’s formula,
Area of the ΔBCD =

= 432 m2
∴ Area of field = 2 × area of the ΔBCD = (2 × 432) m2 = 864 m2
Thus, the area of the grass field that each cow will be getting = (864/18) m2 = 48 m2
6. An umbrella is made by stitching 10 triangular pieces of cloth of two different colours (see Fig.12.16), each piece measuring 20 cm, 50 cm and 50 cm. How much cloth of each colour is required for the umbrella?

Solution:
For each triangular piece, The semi perimeter will be
s = (50+50+20)/2 cm = 120/2 cm = 60cm
Using Heron’s formula,
Area of the triangular piece
=

= √[60(60-50)(60-50)(60-20)] cm2
= √[60×10×10×40] cm2
= 200√6 cm2
∴ The area of all the triangular pieces = 5 × 200√6 cm2 = 1000√6 cm2
7. A kite in the shape of a square with a diagonal 32 cm and an isosceles triangle of base 8 cm and sides 6 cm each is to be made of three different shades as shown in Fig. 12.17. How much paper of each shade has been used in it?

Solution:
As the kite is in the shape of a square, its area will be
A = (½)×(diagonal)2
Area of the kite = (½)×32×32 = 512 cm2.
The area of shade I = Area of shade II
512/2 cm2 = 256 cm2
So, the total area of the paper that is required in each shade = 256 cm2
For the triangle section (III),
The sides are given as 6 cm, 6 cm and 8 cm
Now, the semi perimeter of this isosceles triangle = (6+6+8)/2 cm = 10 cm
By using Heron’s formula, the area of the III triangular piece will be
=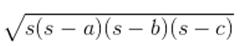
= √[10(10-6)(10-6)(10-8)] cm2
= √(10×4 ×4×2) cm2
= 8√5 cm2 = 17.92 cm2 (approx.)
8. A floral design on a floor is made up of 16 tiles which are triangular, the sides of the triangle being 9 cm, 28 cm and 35 cm (see Fig. 12.18). Find the cost of polishing the tiles at the rate of 50p per cm2 .

Solution:
The semi perimeter of the each triangular shape = (28+9+35)/2 cm = 36 cm
By using Heron’s formula,
The area of each triangular shape will be

= 36√6 cm2 = 88.2 cm2
Now, the total area of 16 tiles = 16×88.2 cm2 = 1411.2 cm2
It is given that the polishing cost of tiles = 50 paise/cm2
∴ The total polishing cost of the tiles = Rs. (1411.2×0.5) = Rs. 705.6

9. A field is in the shape of a trapezium whose parallel sides are 25 m and 10 m. The non-parallel sides are 14 m and 13 m. Find the area of the field.
Solution:
First, draw a line segment BE parallel to the line AD. Then, from B, draw a perpendicular on the line segment CD.

Now, it can be seen that the quadrilateral ABED is a parallelogram. So,
AB = ED = 10 m
AD = BE = 13 m
EC = 25-ED = 25-10 = 15 m
Now, consider the triangle BEC,
Its semi perimeter (s) = (13+14+15)/2 = 21 m
By using Heron’s formula,
Area of ΔBEC =

= 84 m2
We also know that the area of ΔBEC = (½)×CE×BF
84 cm2 = (½)×15×BF
BF = (168/15) cm = 11.2 cm
So, the total area of ABED will be BF×DE i.e. 11.2×10 = 112 m2
∴ Area of the field = 84+112 = 196 m2
| Also Access |
| NCERT Exemplar for Class 9 Maths Chapter 12 |
| CBSE Notes for Class 9 Maths Chapter 12 |
Chapter 12 Heron’s Formula belongs to Unit 5: Mensuration. This unit carries a total of 13 marks out of 100. Therefore, this is an important chapter and should be studied thoroughly. The important topics that are covered in this chapter are:
- Area of a Triangle – by Heron’s Formula
- Application of Heron’s Formula in Finding Areas of Quadrilaterals
Heron’s formula helps us to find the area of a triangle with 3 side lengths. Besides the formula, Heron also contributed in other ways – the most notable one being the inventor of the very first steam engine called the Aeolipile. However, Heron couldn’t find any practical applications for it; instead, it ended up being used as a toy and an object of curiosity for the ancient Greeks.
Explore more about Heron’s Formula and learn how to solve various kinds of problems only on NCERT Solutions For Class 9 Maths. It is also one of the best academic resources to revise for your exams.
Key Features of NCERT Solutions for Class 9 Maths Chapter 12 Heron’s Formula
- Well-structured content
- Relevant formulas are highlighted
- Easy-to-understand language and jargon-free explanations
- Designed by qualified teachers
- Latest questions with solutions from the updated syllabus
- A thorough analysis of previous year question papers
- Access to other learning resources, such as sample papers and more
The expert faculty team of members have formulated the solutions in a lucid manner to improve the problem-solving abilities of the students. For a more clear idea about Heron’s Formula, students can refer to the study materials available at BYJU’S.
Disclaimer:
Dropped Topics – 12.1 Introduction and 12.3 Application of Heron’s formula in finding areas of quadrilaterals.
Frequently Asked Questions on NCERT Solutions for Class 9 Maths Chapter 12
What is the main aim of NCERT Solutions for Class 9 Maths Chapter 12?
What are the key benefits of learning NCERT Solutions for Class 9 Maths Chapter 12?
1. Students can easily access the solutions for each exercise from the chapters available.
2. The solutions also provide graphs and illustrations that help to understand the concepts clearly.
3. These solutions are prepared by BYJU’S expert team focussing on accuracy.














Nice