* According to the revised NCERT Syllabus 2023-24 update, this chapter has been removed.
NCERT Solutions for Class 9 Maths Chapter 11 Constructions is provided here for the benefit of students of Class 9. Geometry is a fundamental concept that is useful in many fields. Therefore, it is necessary to learn the concept and understand its applications. The best way to learn this concept is by referring to the NCERT Solutions for Class 9 Maths Chapter 11 Constructions. These solutions are designed by teachers who can articulate concepts in an efficient manner to help students ace their CBSE Class 9 Maths examination.
Hence, NCERT Solutions is the guide you should adopt for your studies, as the content is presented in a comprehensive format. We ensure that the instructions provided are simple and clear-cut. Moreover, we ensure that our content is updated as per the latest CBSE Syllabus 2023-24 and guidelines.
Download PDF of NCERT Solutions Class 9 Maths Chapter 11 Constructions
List of Exercises in Class 9 Maths Chapter 11:
Access Answers of NCERT Class 9 Maths Chapter 11 – Constructions
Exercise 11.1 Page: 191
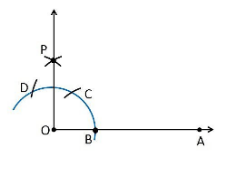
1. Construct an angle of 90° at the initial point of a given ray and justify the construction.
Construction Procedure:
To construct an angle 90°, follow the given steps:
1. Draw a ray OA.
2. Take O as a centre with any radius, and draw an arc DCB that cuts OA at B.
3. With B as a centre with the same radius, mark a point C on the arc DCB.
4. With C as a centre and the same radius, mark a point D on the arc DCB.
5. Take C and D as the centres, and draw two arcs which intersect each other with the same radius at P.
6. Finally, the ray OP is joined, which makes an angle of 90° with OA.
Justification
To prove ∠POA = 90°
In order to prove this, draw a dotted line from the point O to C and O to D, and the angles formed are:
From the construction, it is observed that
OB = BC = OC
Therefore, OBC is an equilateral triangle
So that, ∠BOC = 60°.
Similarly,
OD = DC = OC
Therefore, DOC is an equilateral triangle
So that, ∠DOC = 60°.
From SSS triangle congruence rule,
△OBC ≅ OCD
So, ∠BOC = ∠DOC [By C.P.C.T]
Therefore, ∠COP = ½ ∠DOC = ½ (60°).
∠COP = 30°
To find the ∠POA = 90°:
∠POA = ∠BOC+∠COP
∠POA = 60°+30°
∠POA = 90°
Hence, justified.
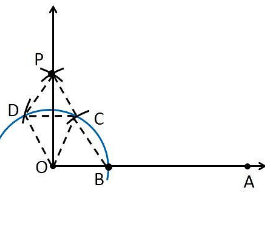
2. Construct an angle of 45° at the initial point of a given ray and justify the construction.
Construction Procedure:
1. Draw a ray OA.
2. Take O as a centre with any radius, draw an arc DCB that cuts OA at B.
3. With B as a centre with the same radius, mark a point C on the arc DCB.
4. With C as a centre and the same radius, mark a point D on the arc DCB.
5. Take C and D as the centres, and draw two arcs which intersect each other with the same radius at P.
6. Finally, the ray OP is joined, which makes an angle of 90° with OA.
7. Take B and Q as the centres, and draw the perpendicular bisector which intersects at the point R
8. Draw a line that joins the points O and R
9. So, the angle formed ∠ROA = 45°

Justification
From the construction,
∠POA = 90°
The perpendicular bisector from points B and Q divides the ∠POA into two halves. So it becomes
∠ROA = ½ ∠POA
∠ROA = (½)×90° = 45°
Hence, justified

Solution:
(i) 30°
Construction Procedure:
1. Draw a ray OA
2. Take O as a centre with any radius, and draw an arc BC which cuts OA at B.
3. With B and C as centres, draw two arcs which intersect each other at point E, and the perpendicular bisector is drawn.
4. Thus, ∠EOA is the required angle making 30° with OA.


Construction Procedure:
1. Draw an angle ∠POA = 90°.
2. Take O as a centre with any radius, and draw an arc BC which cuts OA at B and OP at Q
3. Now, draw the bisector from points B and Q, where it intersects at the point R such that it makes an angle ∠ROA = 45°.
4. Again, ∠ROA is bisected such that ∠TOA is formed, which makes an angle of 22.5° with OA

(iii) 15°
Construction Procedure:
1. An angle ∠DOA = 60° is drawn.
2. Take O as the centre with any radius, and draw an arc BC which cuts OA at B and OD at C
3. Now, draw the bisector from points B and C, where it intersects at point E such that it makes an angle ∠EOA = 30°.
4. Again, ∠EOA is bisected such that ∠FOA is formed, which makes an angle of 15° with OA.
5. Thus, ∠FOA is the required angle making 15° with OA.

4. Construct the following angles and verify by measuring them with a protractor:
(i) 75° (ii) 105° (iii) 135°
Solution:
(i) 75°
Construction Procedure:
1. A ray OA is drawn.
2. With O as the centre, draw an arc of any radius and intersect at point B on the ray OA.
3. With B as the centre, draw an arc C, and with C as the centre, draw an arc D.
4. With D and C as the centres, draw an arc that intersects at point P.
5. Join points O and P.
6. The point that the arc intersects the ray OP is taken as Q.
7. With Q and C as the centres, draw an arc that intersects at point R.
8. Join points O and R.
9. Thus, ∠AOE is the required angle making 75° with OA.

(ii) 105°
Construction Procedure:
1. A ray OA is drawn.
2. With O as the centre, draw an arc of any radius and intersect at point B on the ray OA.
3. With B as the centre, draw an arc C, and with C as the centre, draw an arc D.
4. With D and C as the centres, draw an arc that intersects at point P.
5. Join the points O and P
6. The point that the arc intersects the ray OP is taken as Q.
7. With Q and D as the centres, draw an arc that intersects at point R.
8. Join points O and R.
9. Thus, ∠AOR is the required angle making 105° with OA.

(iii) 135°
Construction Procedure:
1. Draw a line AOA‘
2. Draw an arc of any radius that cuts the line AOA‘ at points B and B‘
3. With B as the centre, draw an arc of the same radius at point C.
4. With C as the centre, draw an arc of the same radius at point D.
5. With D and C as the centres, draw an arc that intersects at point P.
6. Join OP.
7. The point that the arc intersects the ray OP is taken as Q, and it forms an angle of 90°.
8. With B‘ and Q as the centre, draw an arc that intersects at point R.
9. Thus, ∠AOR is the required angle making 135° with OA.

5. Construct an equilateral triangle, given its side and justify the construction.
Construction Procedure:
1. Let us draw a line segment AB = 4 cm.
2. With A and B as centres, draw two arcs on the line segment AB and note the point as D and E.
3. With D and E as centres, draw the arcs that cut the previous arc respectively that forms an angle of 60° each.
4. Now, draw the lines from A and B that are extended to meet each other at point C.
5. Therefore, ABC is the required triangle.

Justification:
From the construction, it is observed that,
AB = 4 cm, ∠A = 60° and ∠B = 60°
We know that the sum of the interior angles of a triangle is equal to 180°
∠A+∠B+∠C = 180°
Substitute the values
⇒ 60°+60°+∠C = 180°
⇒ 120°+∠C = 180°
⇒∠C = 60°
While measuring the sides, we get,
BC = CA = 4 cm (Sides opposite to equal angles are equal)
AB = BC = CA = 4 cm
∠A = ∠B = ∠C = 60°
Hence, justified.
Exercise 11.2 Page: 195
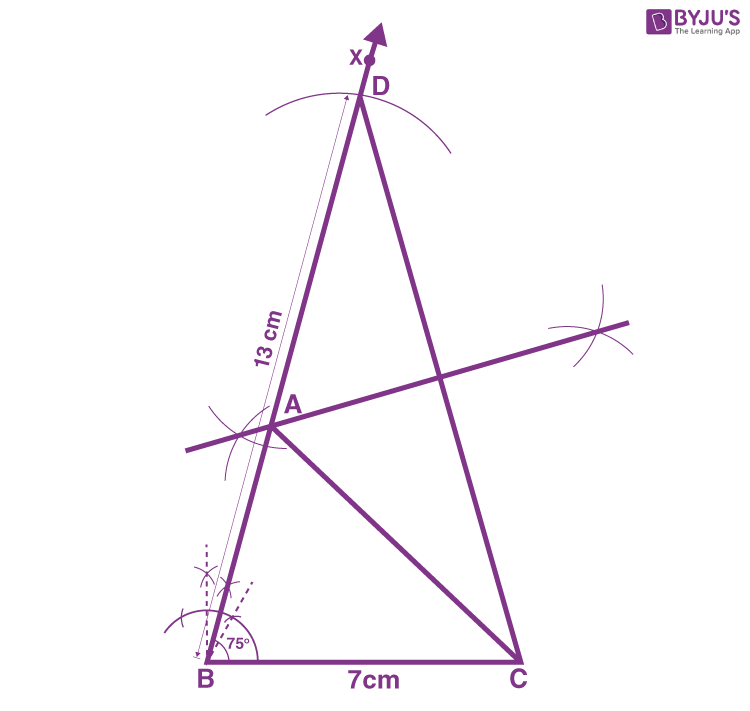
1. Construct a triangle ABC in which BC = 7cm, ∠B = 75° and AB+AC = 13 cm.
Construction Procedure:
The steps to draw the triangle of the given measurement are as follows:
1. Draw a line segment of base BC = 7 cm.
2. Measure and draw ∠B = 75° and draw the ray BX.
3. Take a compass and measure AB+AC = 13 cm.
4. With B as the centre, draw an arc at the point D.
5. Join DC.
6. Now draw the perpendicular bisector of the line DC, and the intersection point is taken as A.
7. Now join AC.
8. Therefore, ABC is the required triangle.
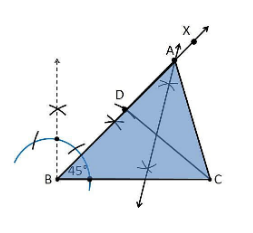
2. Construct a triangle ABC in which BC = 8cm, ∠B = 45° and AB–AC = 3.5 cm.
Construction Procedure:
The steps to draw the triangle of the given measurement are as follows:
1. Draw a line segment of base BC = 8 cm
2. Measure and draw ∠B = 45° and draw the ray BX
3. Take a compass and measure AB-AC = 3.5 cm.
4. With B as the centre, draw an arc at point D on the ray BX.
5. Join DC.
6. Now draw the perpendicular bisector of the line CD, and the intersection point is taken as A.
7. Now join AC.
8. Therefore, ABC is the required triangle.
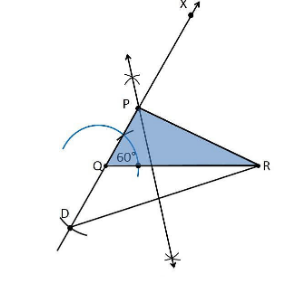
3. Construct a triangle PQR in which QR = 6cm, ∠Q = 60° and PR–PQ = 2cm.
Construction Procedure:
The steps to draw the triangle of the given measurement are as follows:
1. Draw a line segment of base QR = 6 cm
2. Measure and draw ∠Q = 60° and let the ray be QX.
3. Take a compass and measure PR–PQ = 2cm.
4. Since PR–PQ is negative, QD will be below the line QR.
5. With Q as the centre, draw an arc at point D on the ray QX.
6. Join DR.
7. Now draw the perpendicular bisector of the line DR and the intersection point is taken as P.
8. Now join PR.
9. Therefore, PQR is the required triangle.
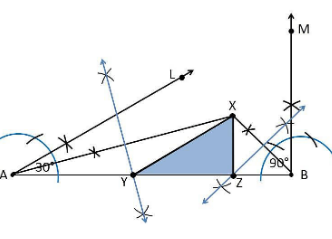
4. Construct a triangle XYZ in which ∠Y = 30°, ∠Z = 90° and XY+YZ+ZX = 11 cm.
Construction Procedure:
The steps to draw the triangle of the given measurement are as follows:
1. Draw a line segment AB which is equal to XY+YZ+ZX = 11 cm.
2. Make an angle ∠LAB = 30° from the point A.
3. Make an angle ∠MBA = 90° from the point B.
4. Bisect ∠LAB and ∠MBA at point X.
5. Now, take the perpendicular bisectors of the lines XA and XB, and the intersection points are Y and Z, respectively.
6. Join XY and XZ.
7. Therefore, XYZ is the required triangle
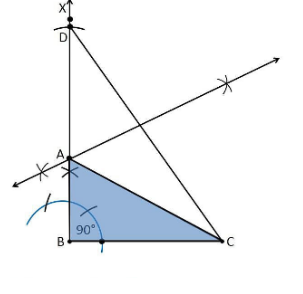
5. Construct a right triangle whose base is 12cm and sum of its hypotenuse and other side is 18 cm.
Construction Procedure:
The steps to draw the triangle of the given measurement are as follows:
1. Draw a line segment of base BC = 12 cm
2. Measure and draw ∠B = 90° and draw the ray BX.
3. Take a compass and measure AB+AC = 18 cm.
4. With B as the centre, draw an arc at point D on the ray BX.
5. Join DC.
6. Now draw the perpendicular bisector of the line CD, and the intersection point is taken as A.
7. Now join AC.
8. Therefore, ABC is the required triangle.
| Also Access |
| NCERT Exemplar for Class 9 Maths Chapter 11 |
| CBSE Notes for Class 9 Maths Chapter 11 |
Chapter 11 Constructions belongs to Unit 4: Geometry. This unit carries a total of 28 marks out of 100. Therefore, this chapter should be studied thoroughly as a majority of the questions could be asked from this unit. The important topics that are covered in this chapter are given below:
- Basic Construction
- Construction of triangles
Constructions is an important chapter included in the board exams of Class 9 Maths that helps the students to understand how different shapes are made. It also teaches their implications and their academic relevance. Learn how to construct a bisector, a perpendicular bisector and much more. Explore more about Constructions and learn to solve various kinds of problems only on NCERT Solutions For Class 9 Maths. It is also one of the best academic resources to revise for your board exams.
Key Features of NCERT Solutions for Class 9 Maths Chapter 11 Constructions
- Formulas are well-explained.
- Comprehensive format and jargon-free language.
- Constant addition of new questions with solutions.
- Additional key tips and tricks are provided.
- Access other important learning resources like sample papers.
Frequently Asked Questions on NCERT Solutions for Class 9 Maths Chapter 11
How are NCERT Solutions for Class 9 Maths Chapter 11 helpful for board exam preparation?
Which is the best source for Class 9 Maths board exam preparation?
What are the main concepts covered in NCERT Solutions for Class 9 Maths Chapter 11?
1. Basic Construction
2. Construction of triangles













It was very helpful!!
Very helpful thank you so much
Very good
Very nice