Faraday’s law of electromagnetic induction, also known as Faraday’s law, is the basic law of electromagnetism which helps us predict how a magnetic field would interact with an electric circuit to produce an electromotive force (EMF). This phenomenon is known as electromagnetic induction.
Michael Faraday proposed the laws of electromagnetic induction in the year 1831. Faraday’s law or the law of electromagnetic induction is the observation or results of the experiments conducted by Faraday. He performed three main experiments to discover the phenomenon of electromagnetic induction.
Faraday’s Laws of Electromagnetic Induction
Faraday’s Laws of Electromagnetic Induction consists of two laws. The first law describes the induction of emf in a conductor and the second law quantifies the emf produced in the conductor. In the next few sections, let us learn these laws in detail.
|
Learn about the experiments that led to the development of Faraday’s Law from the below article: |
Faraday’s First Law of Electromagnetic Induction
The discovery and understanding of electromagnetic induction are based on a long series of experiments carried out by Faraday and Henry. From the experimental observations, Faraday concluded that an emf is induced when the magnetic flux across the coil changes with time. Therefore, Faraday’s first law of electromagnetic induction states the following:
Whenever a conductor is placed in a varying magnetic field, an electromotive force is induced. If the conductor circuit is closed, a current is induced, which is called induced current.
Changing the Magnetic Field Intensity in a Closed Loop
Magnetic field intensity in a closed loop
- By rotating the coil relative to the magnet.
- By moving the coil into or out of the magnetic field.
- By changing the area of a coil placed in the magnetic field.
- By moving a magnet towards or away from the coil.
Faraday’s Second Law of Electromagnetic Induction
Faraday’s second law of electromagnetic induction states that
The induced emf in a coil is equal to the rate of change of flux linkage.
The flux linkage is the product of the number of turns in the coil and the flux associated with the coil. The formula of Faraday’s law is given below:
\(\begin{array}{l}\varepsilon =-N\frac{\Delta \phi }{\Delta t}\end{array} \) |
Where ε is the electromotive force, Φ is the magnetic flux, and N is the number of turns.
Learn more about Faraday’s Law of induction and the relationship between the electric circuit and magnetic field by watching this engaging video from BYJU’S.

Lenz’s Law
The German physicist Heinrich Friedrich Lenz deduced a rule known as Lenz’s law that describes the polarity of the induced emf.
Lenz’s law states that “The polarity of induced emf is such that it tends to produce a current which opposes the change in magnetic flux that produced it.”
The negative sign in the formula represents this effect. Thus, the negative sign indicates that the direction of the induced emf and the change in the direction of magnetic fields have opposite signs.
Read more: Lenz’s law
Faraday’s Law Derivation
Consider a magnet approaching a coil. Consider two-time instances T1 and T2.
Flux linkage with the coil at the time T1 is given by NΦ1.
Flux linkage with the coil at the time T2 is given by NΦ2
Change in the flux linkage is given by
N(Φ2 – Φ1)
Let us consider this change in flux linkage as
Φ = Φ2 – Φ1
Hence, the change in flux linkage is given by
NΦ
The rate of change of flux linkage is given by
NΦ/t
Taking the derivative of the above equation, we get
N dΦ/dt
According to Faraday’s second law of electromagnetic induction, we know that the induced emf in a coil is equal to the rate of change of flux linkage. Therefore,
Considering Lenz’s law,
From the above equation, we can conclude the following
- Increase in the number of turns in the coil increases the induced emf
- Increasing the magnetic field strength increases the induced emf
- Increasing the speed of the relative motion between the coil and the magnet, results in the increased emf
Faraday’s Experiment: Relationship Between Induced EMF and Flux
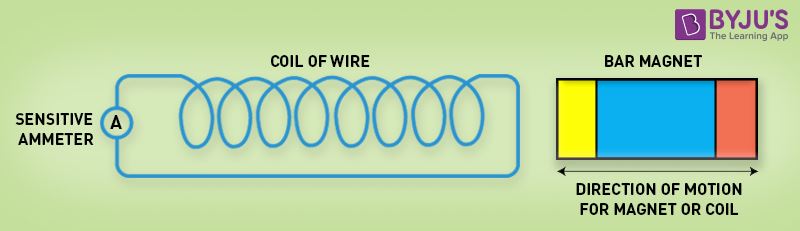
- In the first experiment, he proved that when the strength of the magnetic field is varied, only then current is induced. An ammeter was connected to a loop of wire; the ammeter deflected when a magnet was moved towards the wire.
-
In the second experiment, he proved that passing a current through an iron rod would make it electromagnetic. He observed that when a relative motion exists between the magnet and the coil, an electromotive force will be induced. When the magnet was held stationary about its axis, no electromotive force was observed, but when the magnet was rotated about its own axis then the induced electromotive force was produced. Thus, there was no deflection in the ammeter when the magnet was held stationary.
-
While conducting the third experiment, he recorded that the galvanometer did not show any deflection and no induced current was produced in the coil when the coil was kept away in a stationary magnetic field. The ammeter deflected in the opposite direction when the magnet was kept away from the loop.
Summarising the above points in a table, we have mapped out the relationship between the position of the magnet and the deflection in the Galvanometer.
| Position of Magnet | Deflection in Galvanometer |
| Magnet at Rest | No deflection in the galvanometer |
| The magnet moves towards the coil | Deflection in the galvanometer in one direction |
| Magnet is held stationary at the same position (near the coil) | No deflection galvanometer |
| The magnet moves away from the coil | Deflection in galvanometer but in the opposite direction |
| The magnet held stationary at the same position (away from the coil) | No deflection in the galvanometer |
Conclusion:
After conducting all the experiments, Faraday finally concluded that if relative motion existed between a conductor and a magnetic field, the flux linkage with a coil changed and this change in flux produced a voltage across a coil.
Faraday law basically states, “when the magnetic flux or the magnetic field changes with time, the electromotive force is produced”. Additionally, Michael Faraday also formulated two laws on the basis of the above experiments.
The below videos help to revise the chapter Magnetic Effects of Electric Current Class 10
 |
 |
Applications of Faraday’s Law
Following are the fields where Faraday’s law finds applications:
- Electrical equipment like transformers works on the basis of Faraday’s law.
- Induction cooker works on the basis of mutual induction, which is based on the principle of Faraday’s law.
- By inducing an electromotive force into an electromagnetic flowmeter, the velocity of the fluids is recorded.
- Electric guitar and electric violin are musical instruments that find an application of Faraday’s law.
- Maxwell’s equation is based on the converse of Faraday’s laws which states that a change in the magnetic field brings a change in the electric field.
|
Related Articles: |
Frequently Asked Questions – FAQs
What does Faraday’s First Law of Electromagnetic Induction state?
Faraday’s first law of electromagnetic induction states, “Whenever a conductor is placed in a varying magnetic field, an electromotive force is induced. Likewise, if the conductor circuit is closed, a current is induced, which is called induced current.”
What does Faraday’s Second Law of Electromagnetic Induction state?
Why are Faraday’s laws important?
What does the negative sign indicate in Faraday’s law of electromagnetic induction formula?
What is meant by EMF?
Stay tuned with BYJU’S for more such interesting articles. Also, register to “BYJU’S – The Learning App” for loads of interactive, engaging Physics-related videos and unlimited academic assist.


I am an older fellow trying to learn; and this is a big help to me.
Thanks from;
r c
The explanation is clear cut. So its so helpful for me to learn .THANK YOU from JB
A nice piece of revision material for exams. Thanks bro. I’m grateful
Differential Form of Maxwell Equations
please explain this topic
Refer to the article below:
https://byjus.com/physics/maxwells-equations/